某东M端登录滑块分析学习

TIP

本分类中所有文章仅代表博主个人学习分享，不用于其他任何目的，不提供完整代码，只做学习笔记，抓包内容、敏感网址、数据接口已进行脱敏处理，如有侵权，请联系博主删除。

分析目标

目标：某东M端登录滑块
网址：aHR0cHM6Ly9wbG9naW4ubS5qZC5jb20vbG9naW4vbG9naW4=

抓包分析

进入之后先清理网站数据再刷新，输入手机号，点击获取验证码，到此开始从后往前分析包

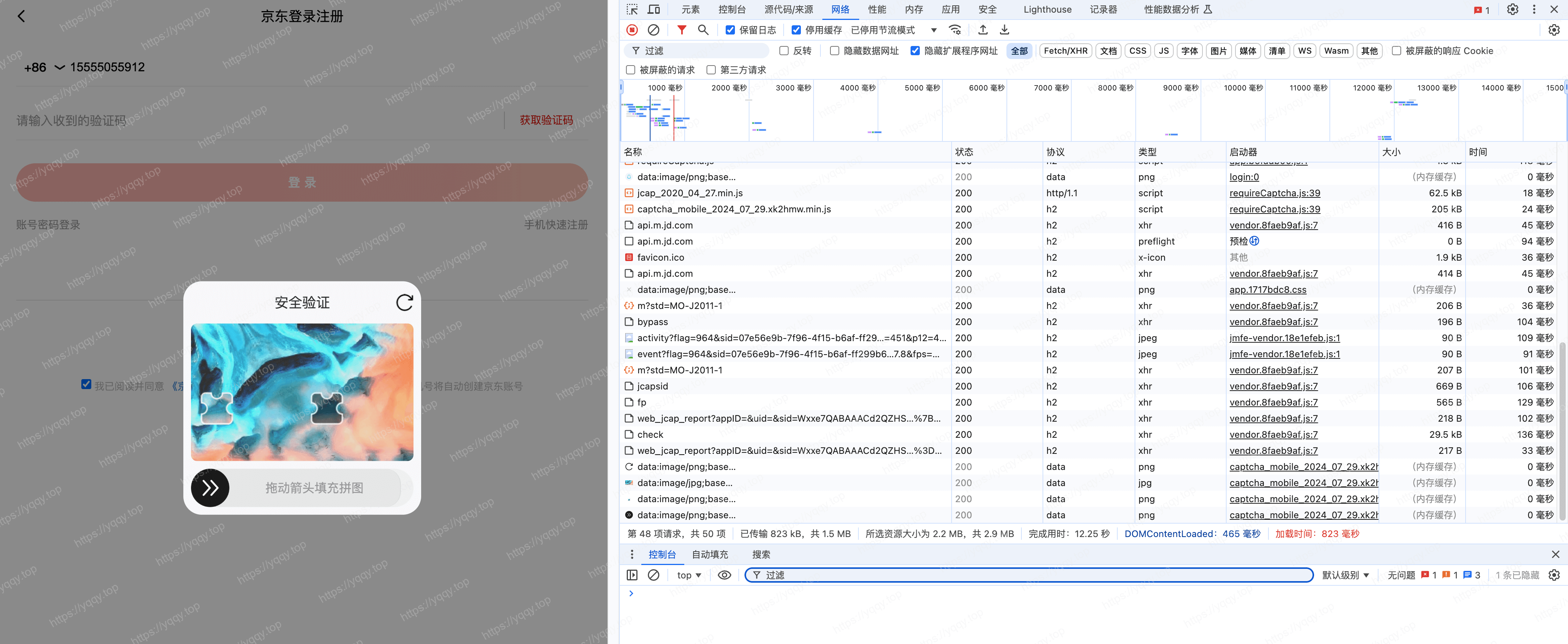
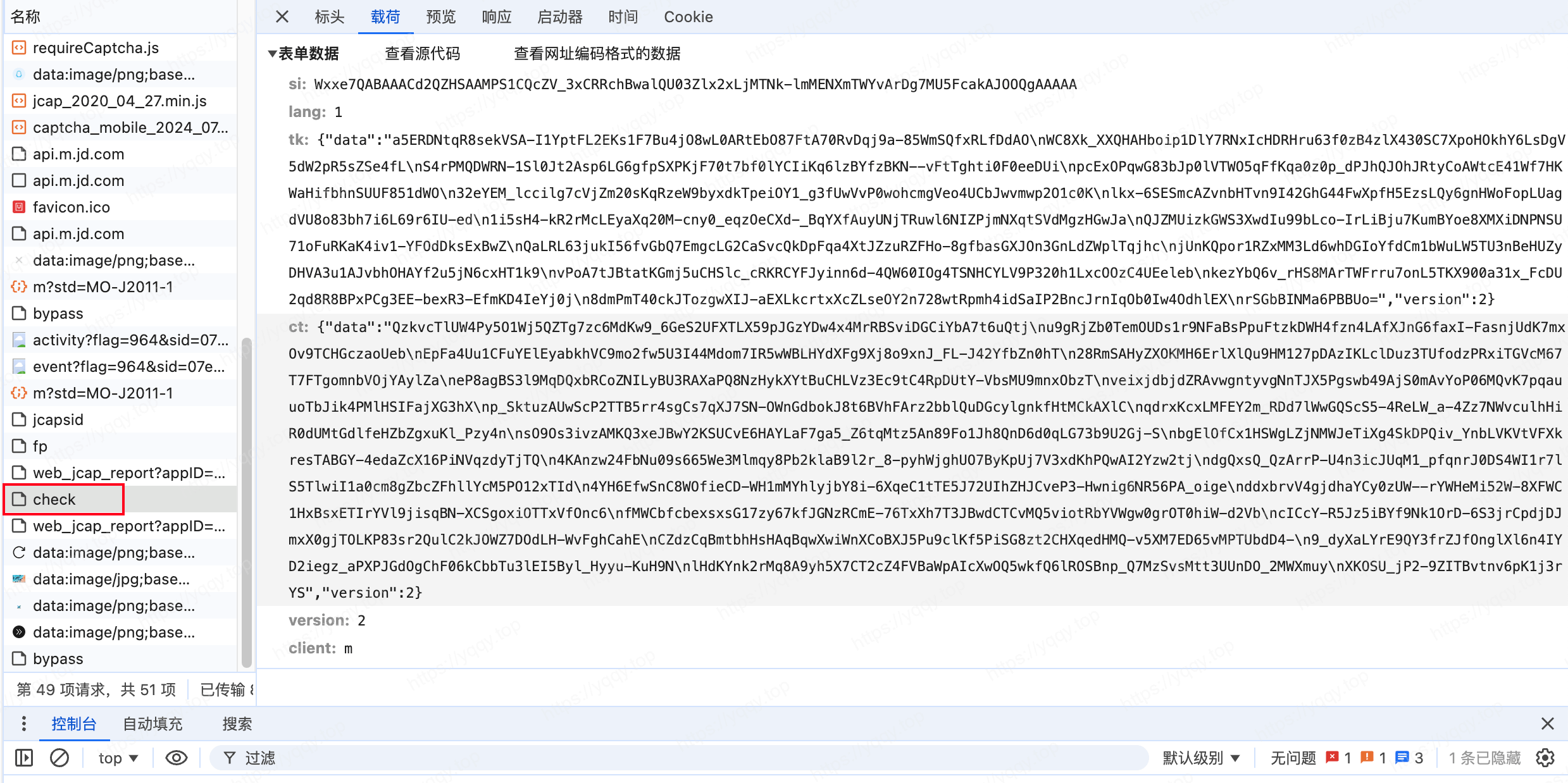
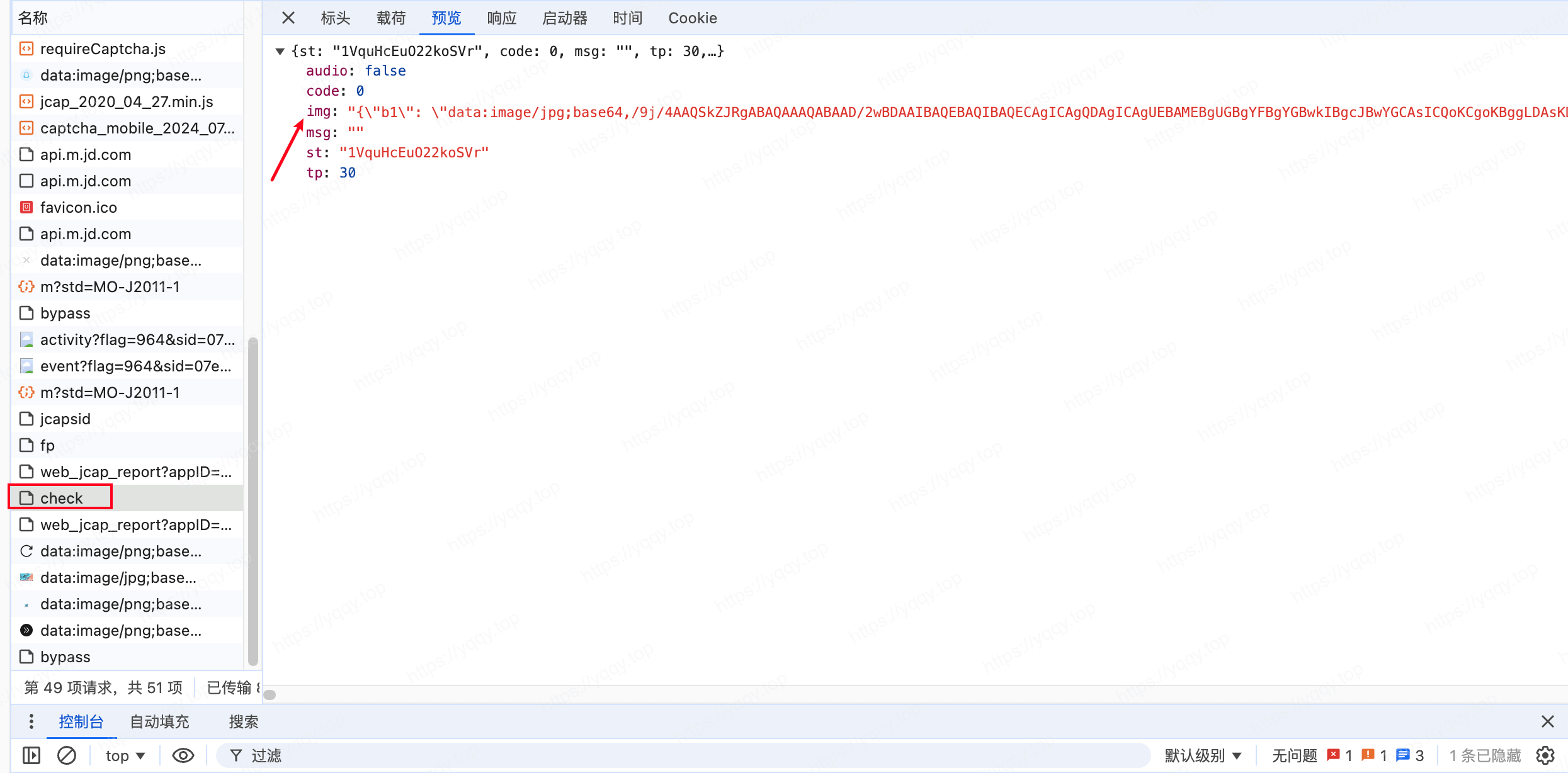
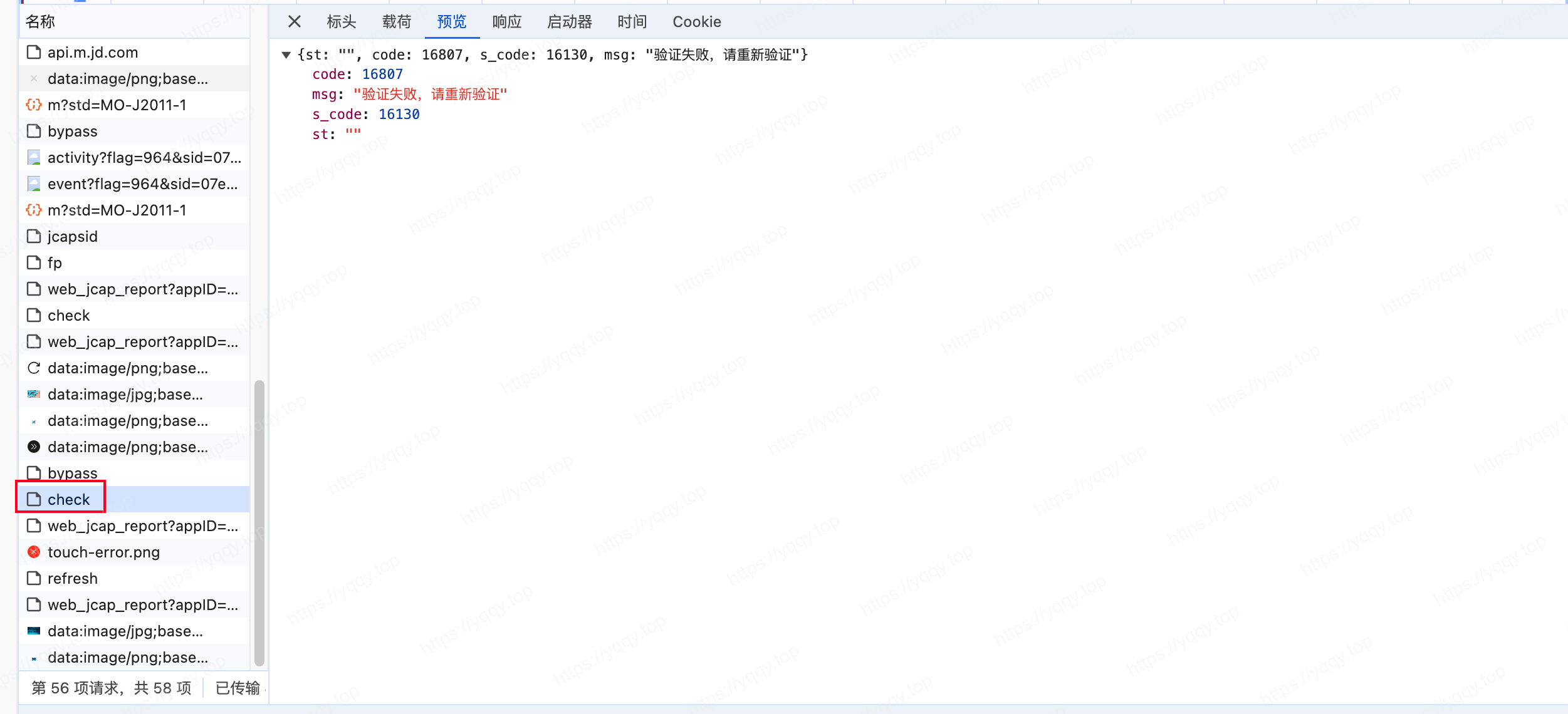
check 接口是获取滑块验证码图片的，也是提交滑块数据的，响应img值里是图片数据，如果提交滑块数据错误会报错

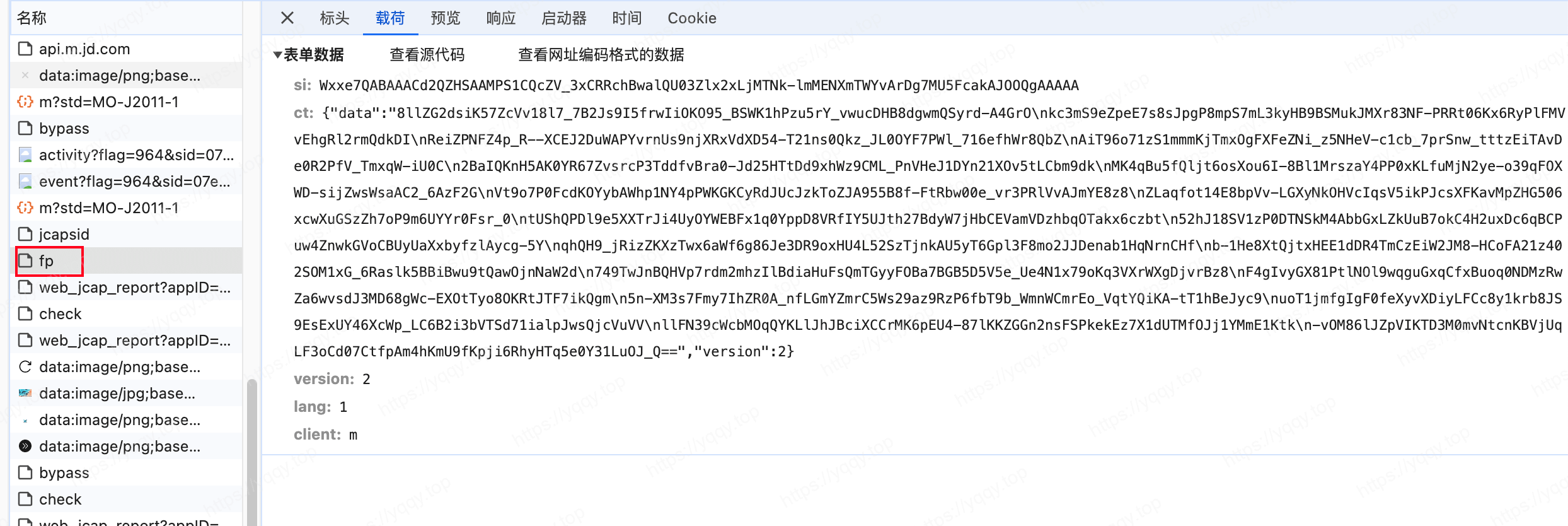
fp 接口里需要知道si（jcapsid接口返回的（jcap_sid））、ct怎么来的，看起来是一些指纹信息

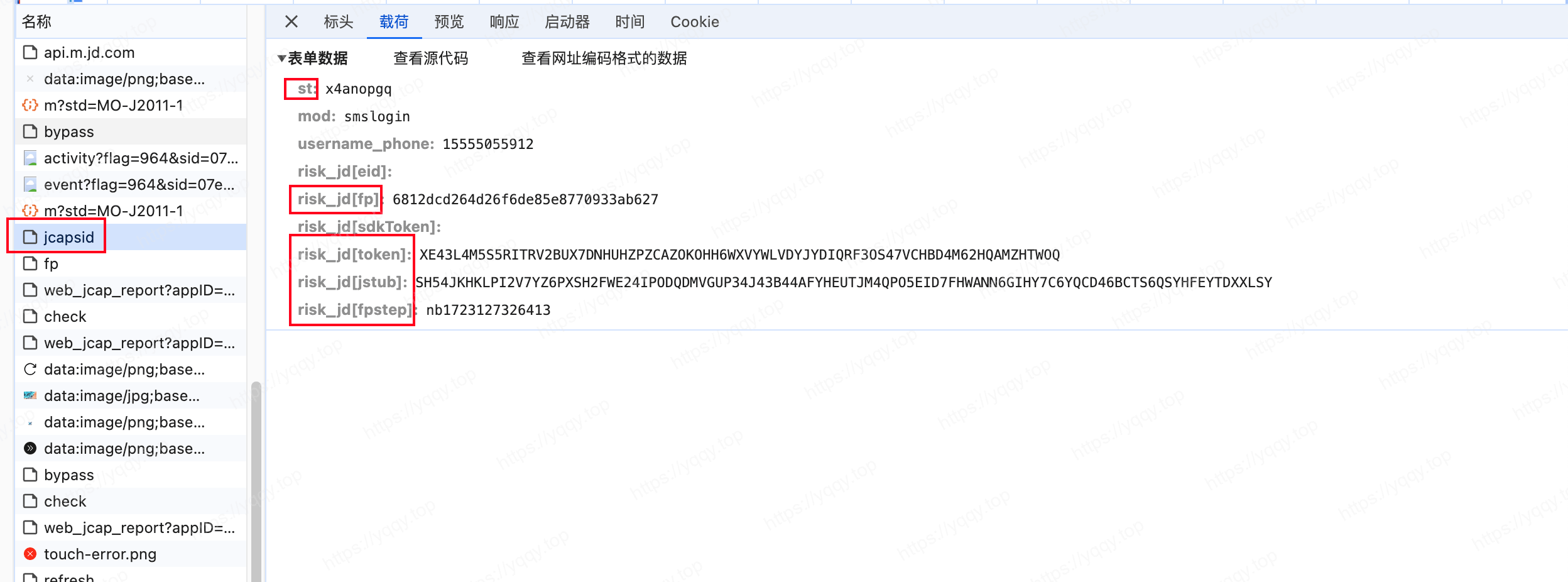
jcapsid 接口需要知道以下参数计算

st: 搜了下在new_login_entrance的响应里
risk_jd[fp]: 需要计算
risk_jd[token]: 搜了下在m.html里
risk_jd[jstub]: 需要计算
risk_jd[fpstep]: nb + 时间戳

逆向分析

所以一共需要分析出以下参数

jcapsid 接口 risk_jd[fp]、risk_jd[jstub]
fp 接口 ct
check 接口 tk、ct

1.jcapsid - risk_jd[fp]

整体搜索一下risk_jd[fp]，搜到几个结果，挨个打开一下，最后定位到了图中所示位置，此时risk_jd[fp]: r.fp，所以要继续看r.fp的值

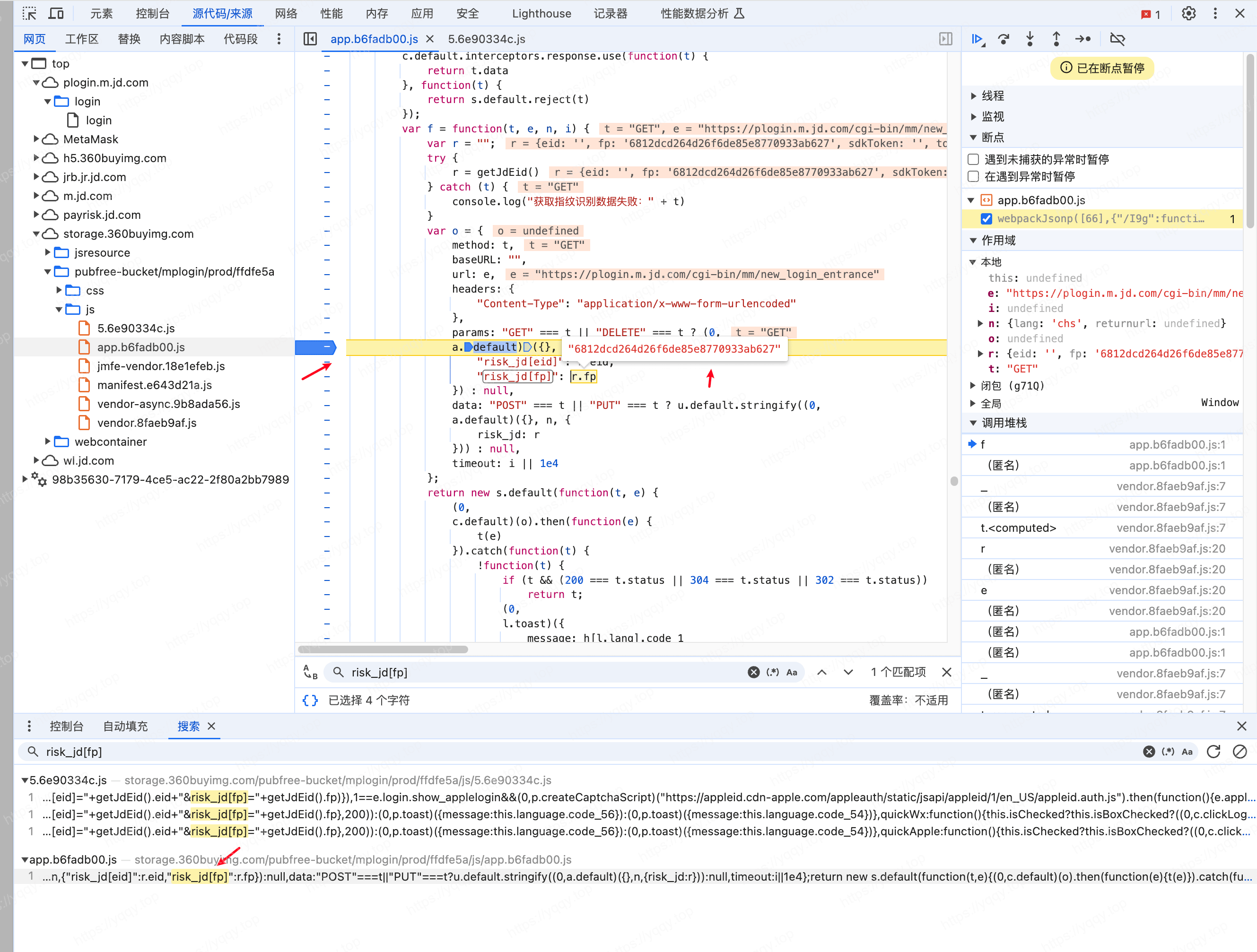
在上方看到r的值，fp属性在其中，通过r = getJdEid()知道r是怎么来的，断点跟入

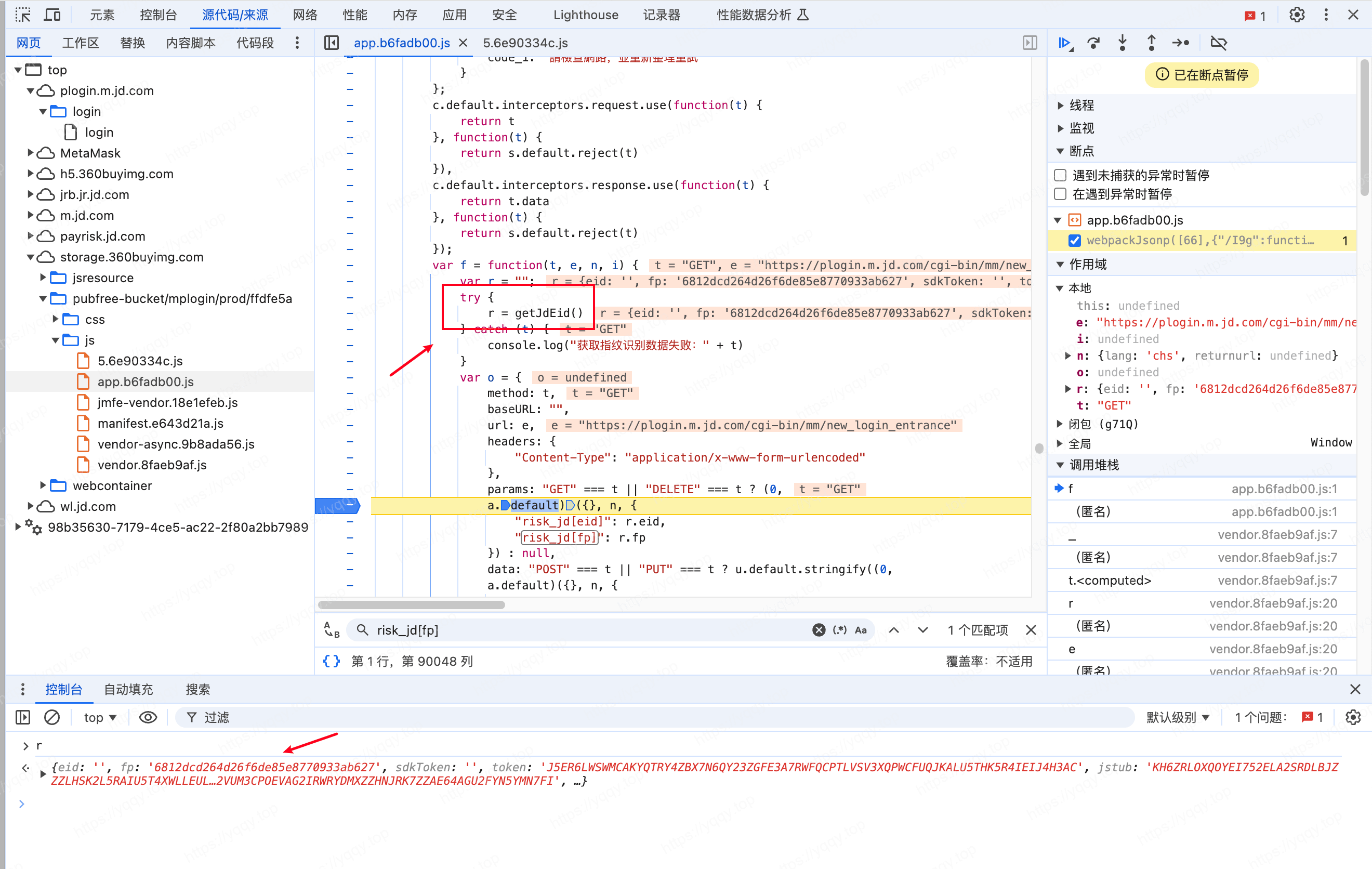
跟进来之后看到fp: risk_jd_local_fingerprint，这就知道怎么来的了

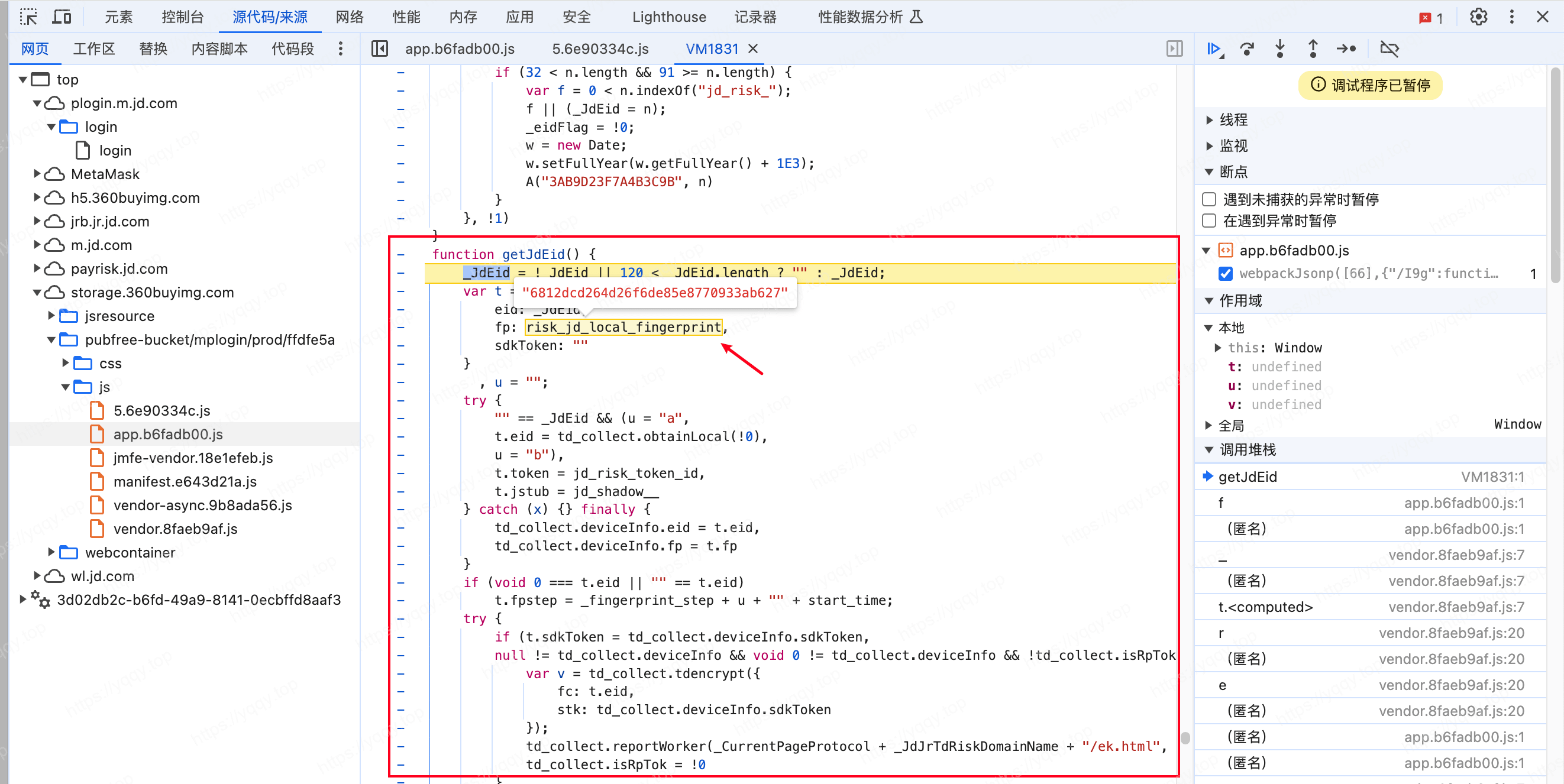
搜一下关键词又发现risk_jd_local_fingerprint = t，且t是函数传进来的，那么就跟一下栈

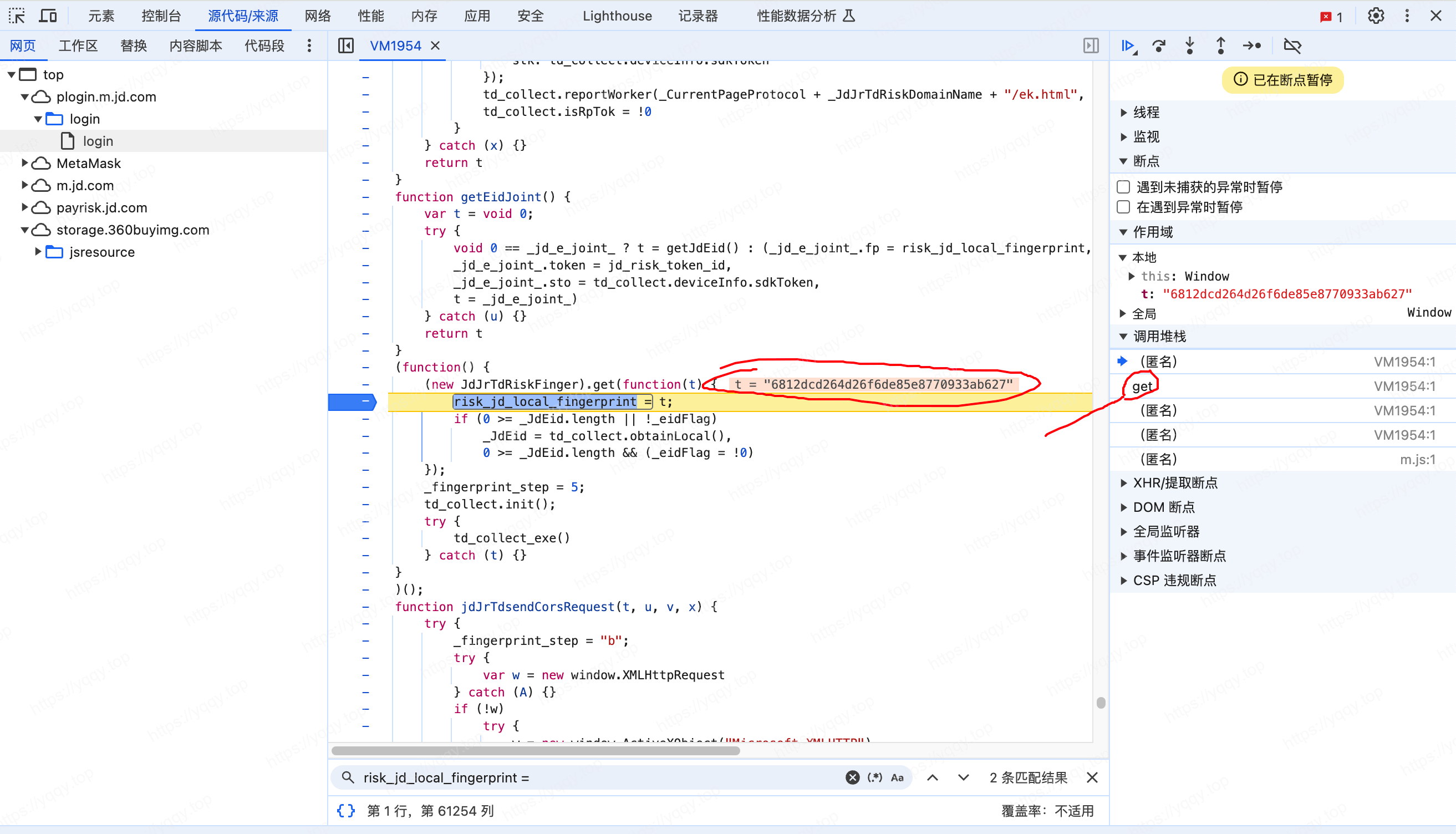
跟进来后看出这个函数参数b就是t，b = this.x64hash128(c.join("~~~", 31);，其中c是各种指纹信息

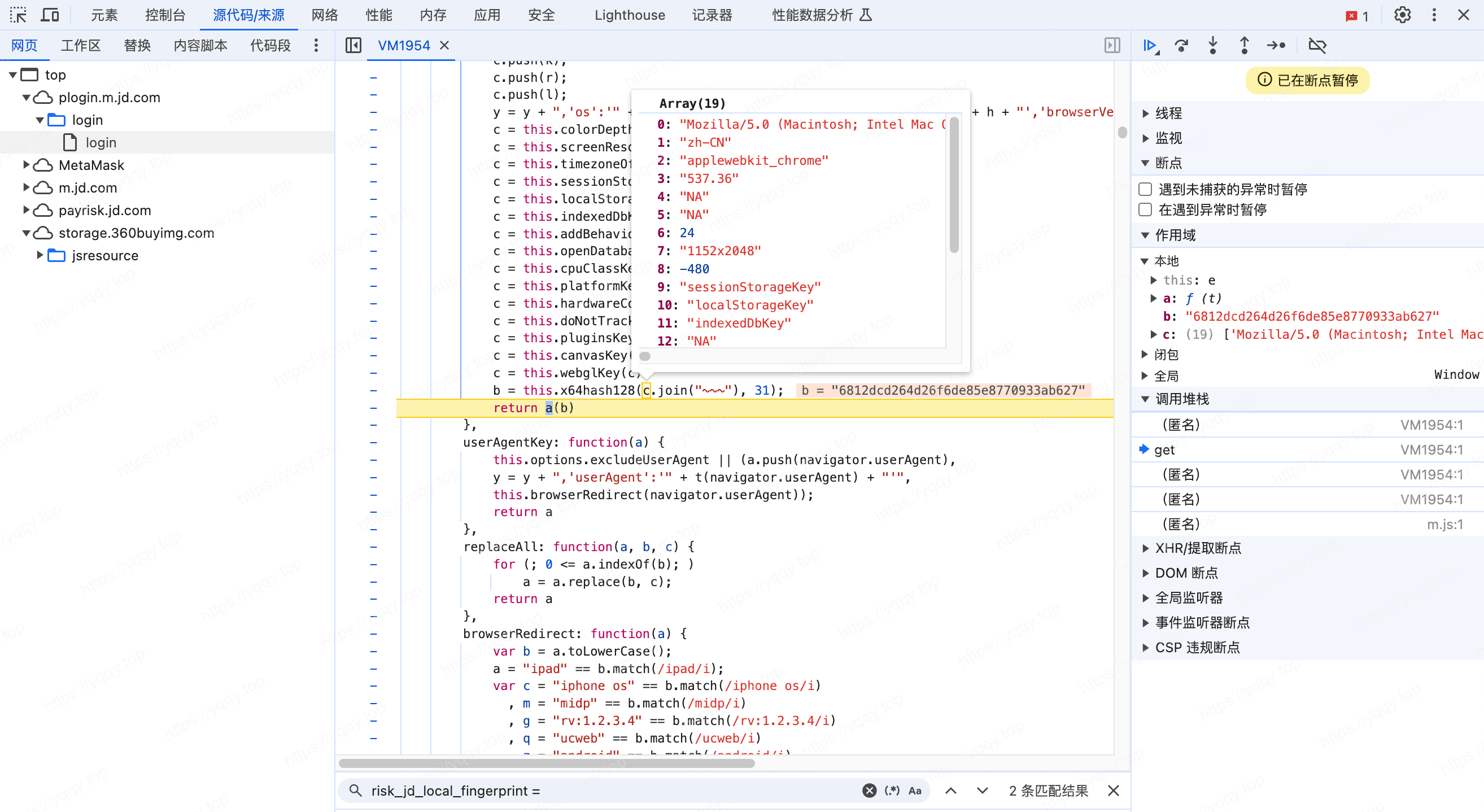
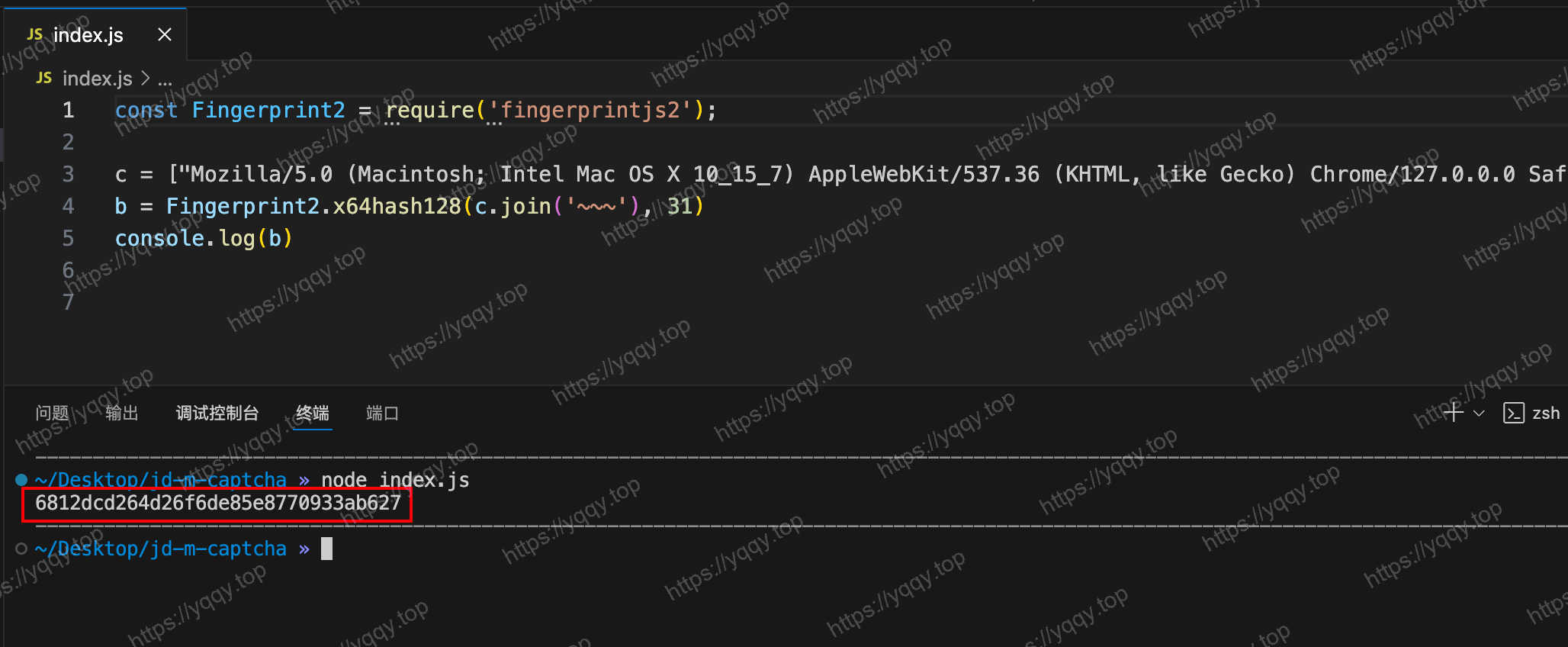
这个x64hash128函数是开源项目 fingerprintjs 的方法，本地模拟一下，成功算出

2.jcapsid - risk_jd[jstub]

和risk_jd[fp]一样，找到js中的位置，看出来jstub的值是jd_shadow__

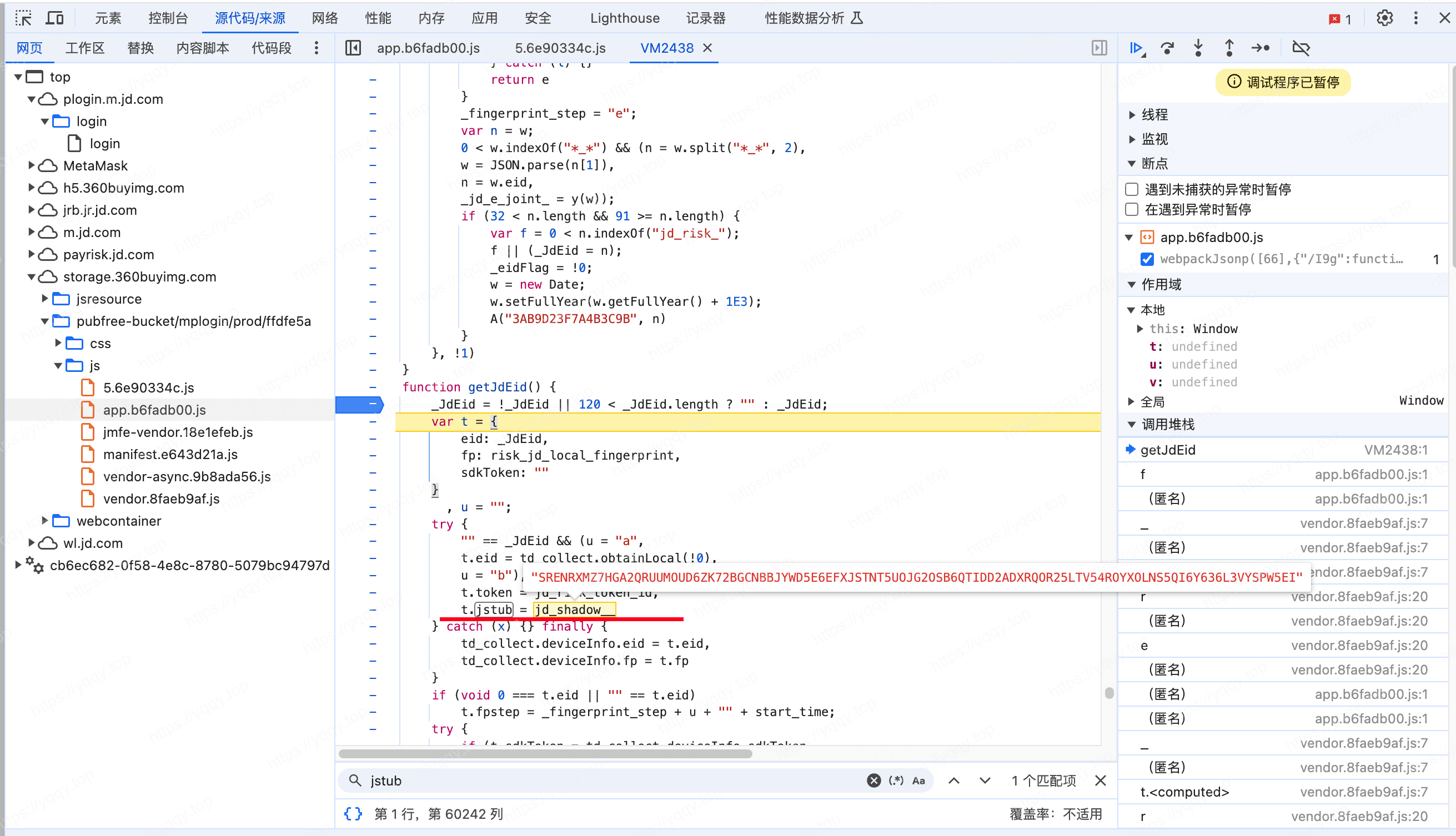
在文件中搜一下来源，看出来是一个AES加密算法，扣一下算法

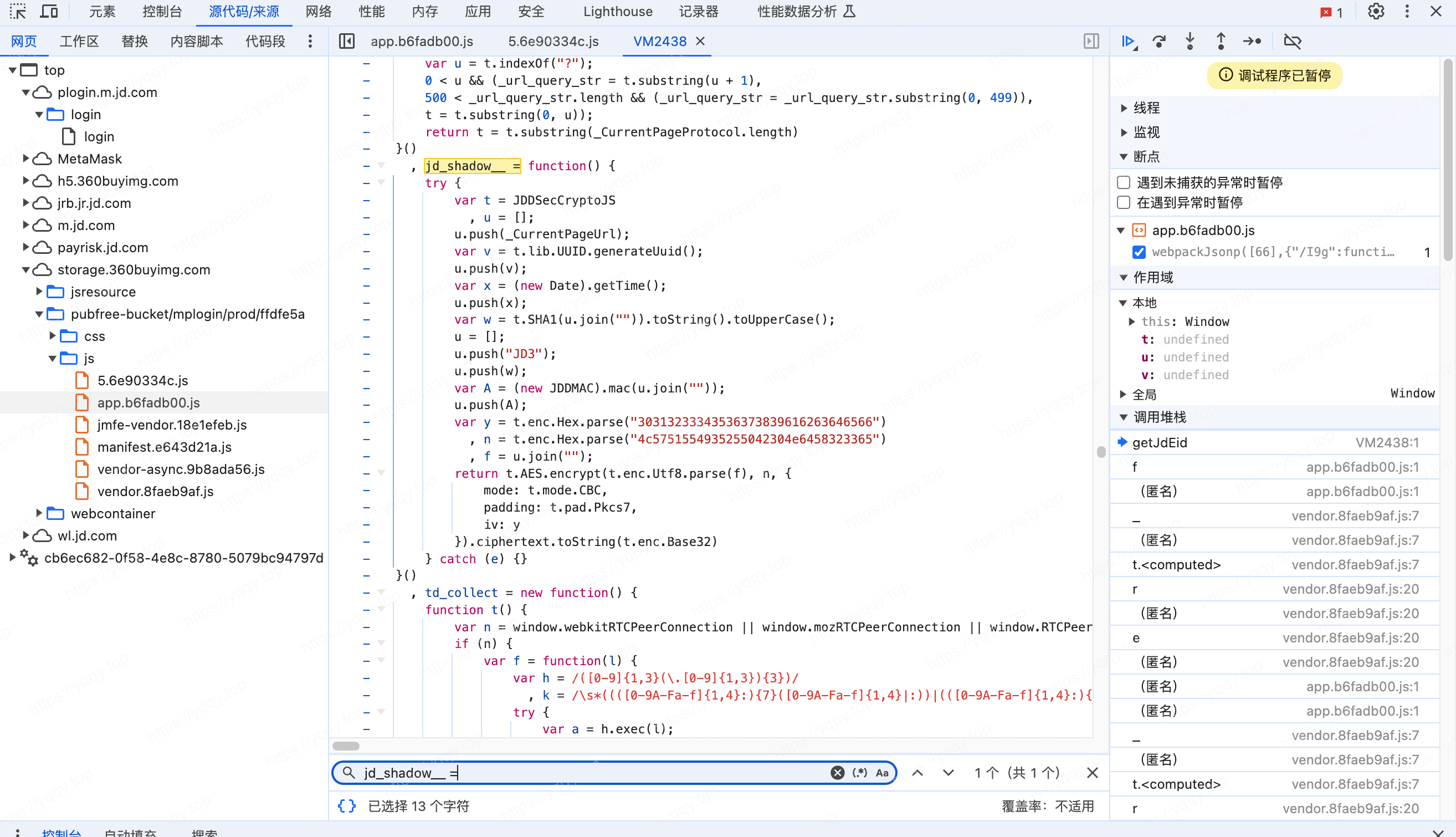
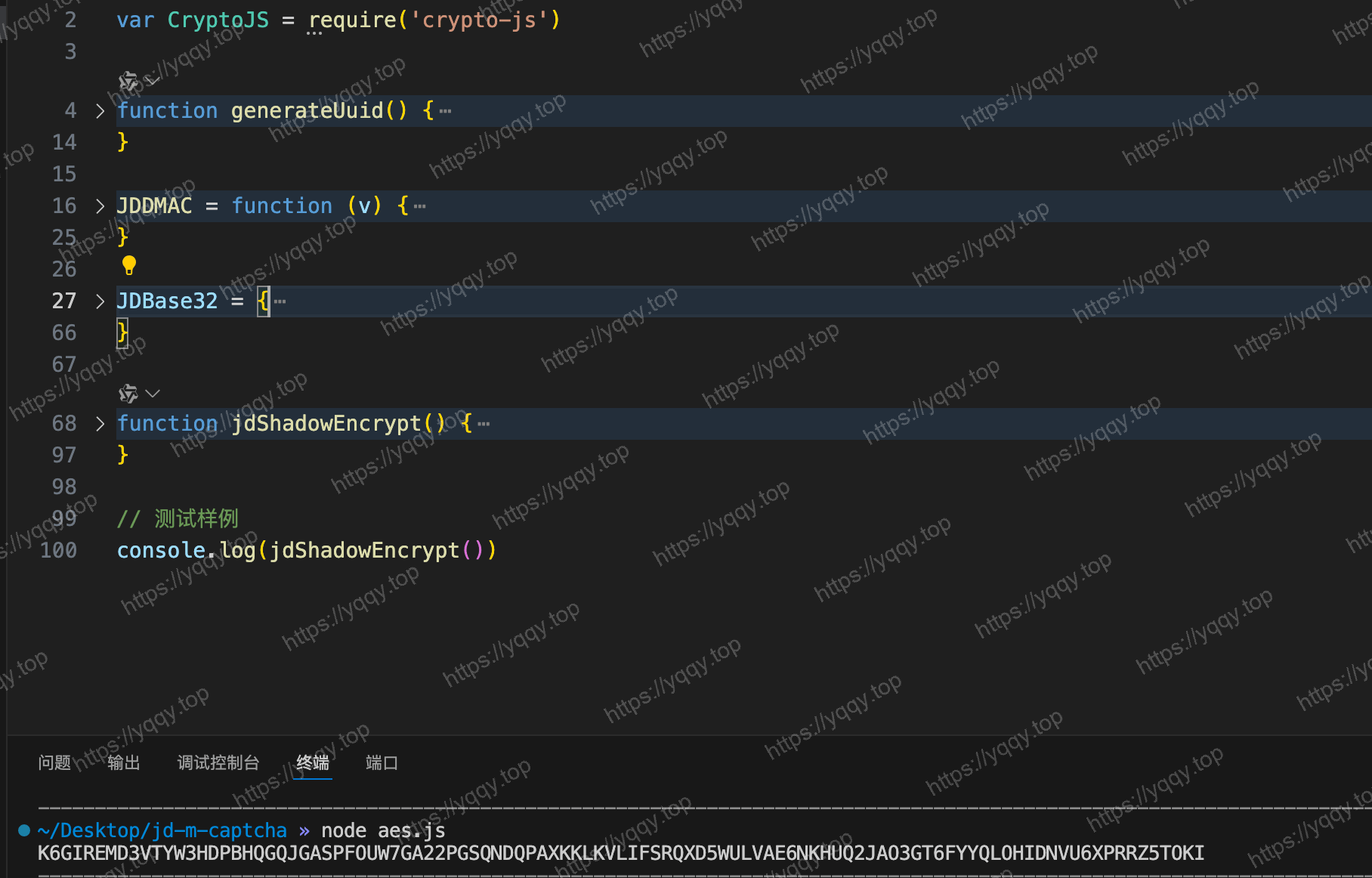
缺啥函数补啥函数，搞定

3.fp - ct

滑块中显示的图片是ct参数

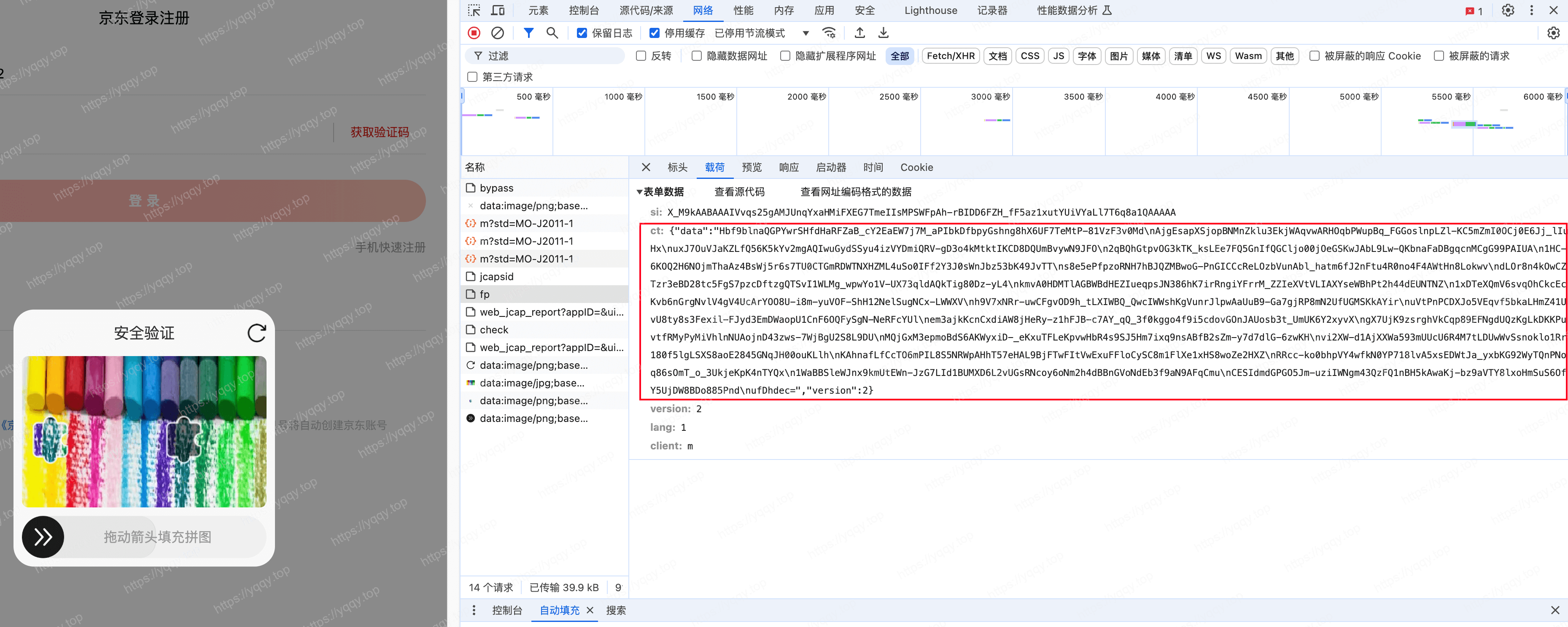
跟一下调用栈

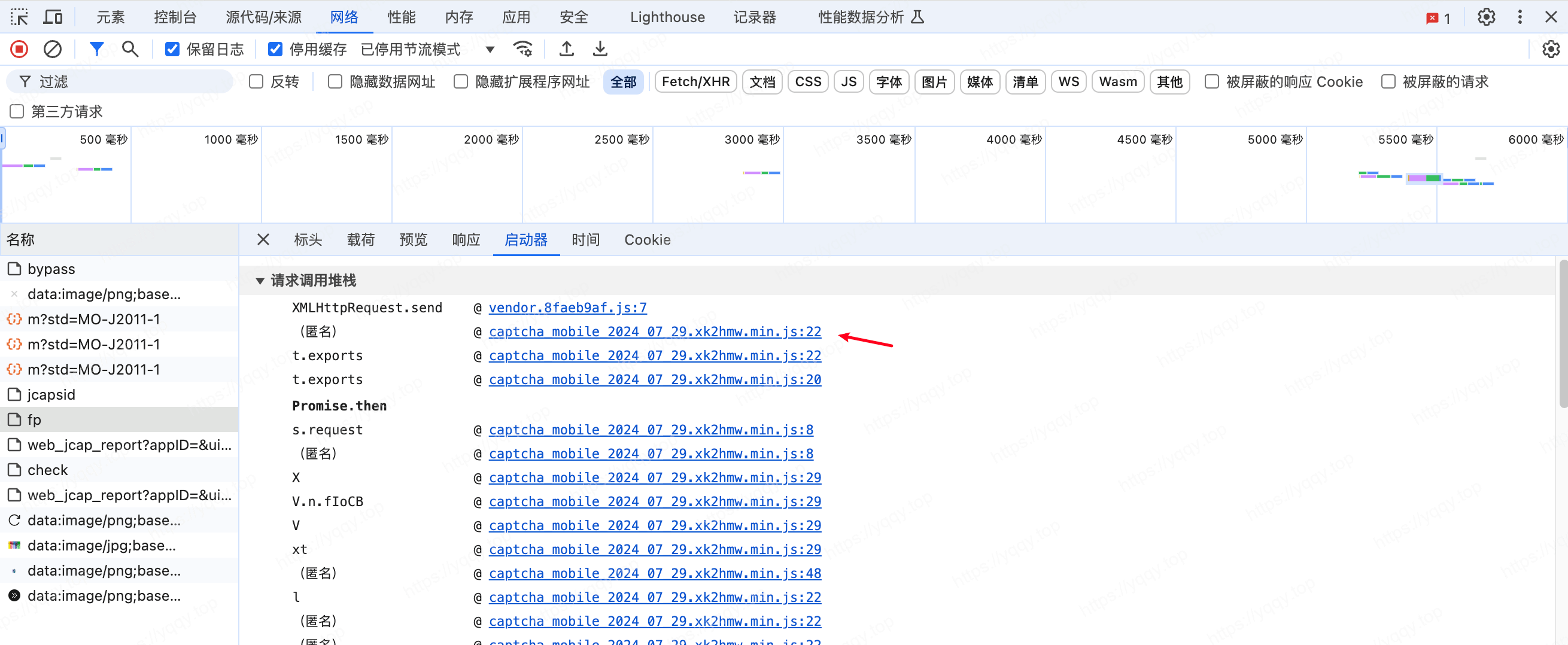
进入js中，搜一下ct =，定位到如图位置
所以ct就是用pt(o.RfeFa(vt, m) + o.FSiZM(gt, y.si[e("0x4c") + "gth"], 4) + y.si + d + c, l, v)计算的

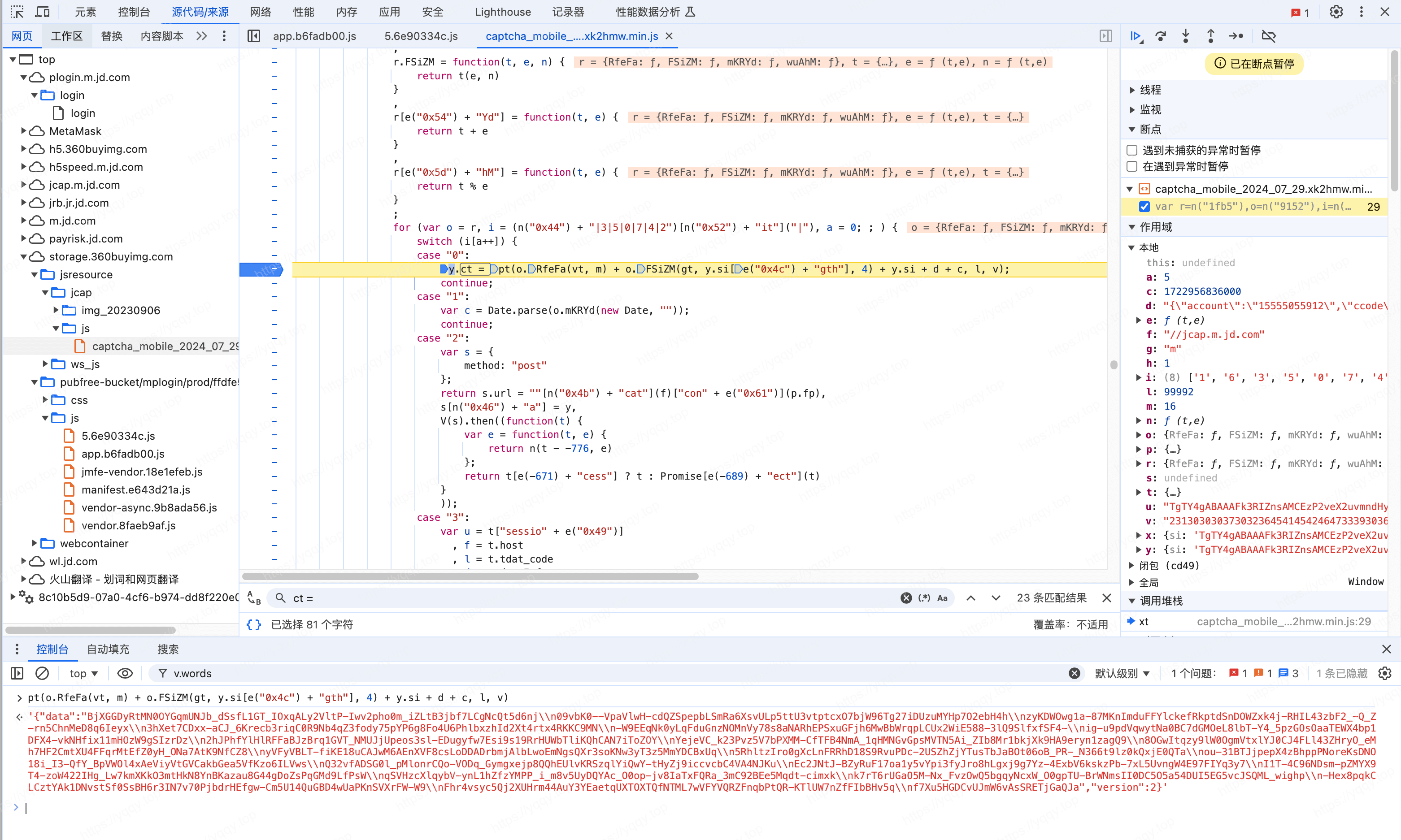
从后往前分别找一下参数，先看参数v，搜一下v的值，发现l和v都在requireCaptcha.js这个文件中

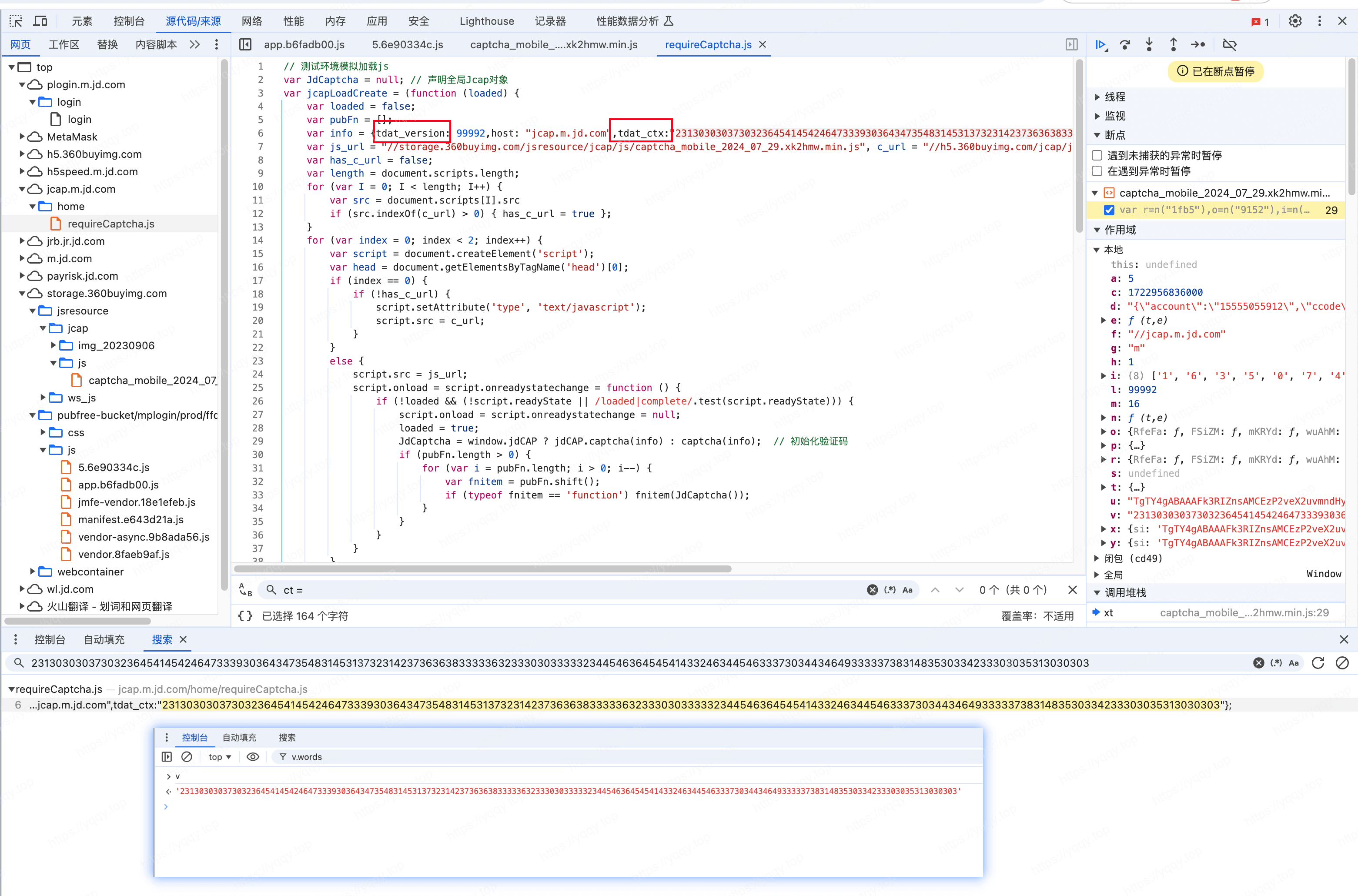
c的值是时间戳，Date.parse(new Date)
d的值看起来是一些手机号，wgl等环境参数
y.si是前文jcapsid接口中的jcap_sid

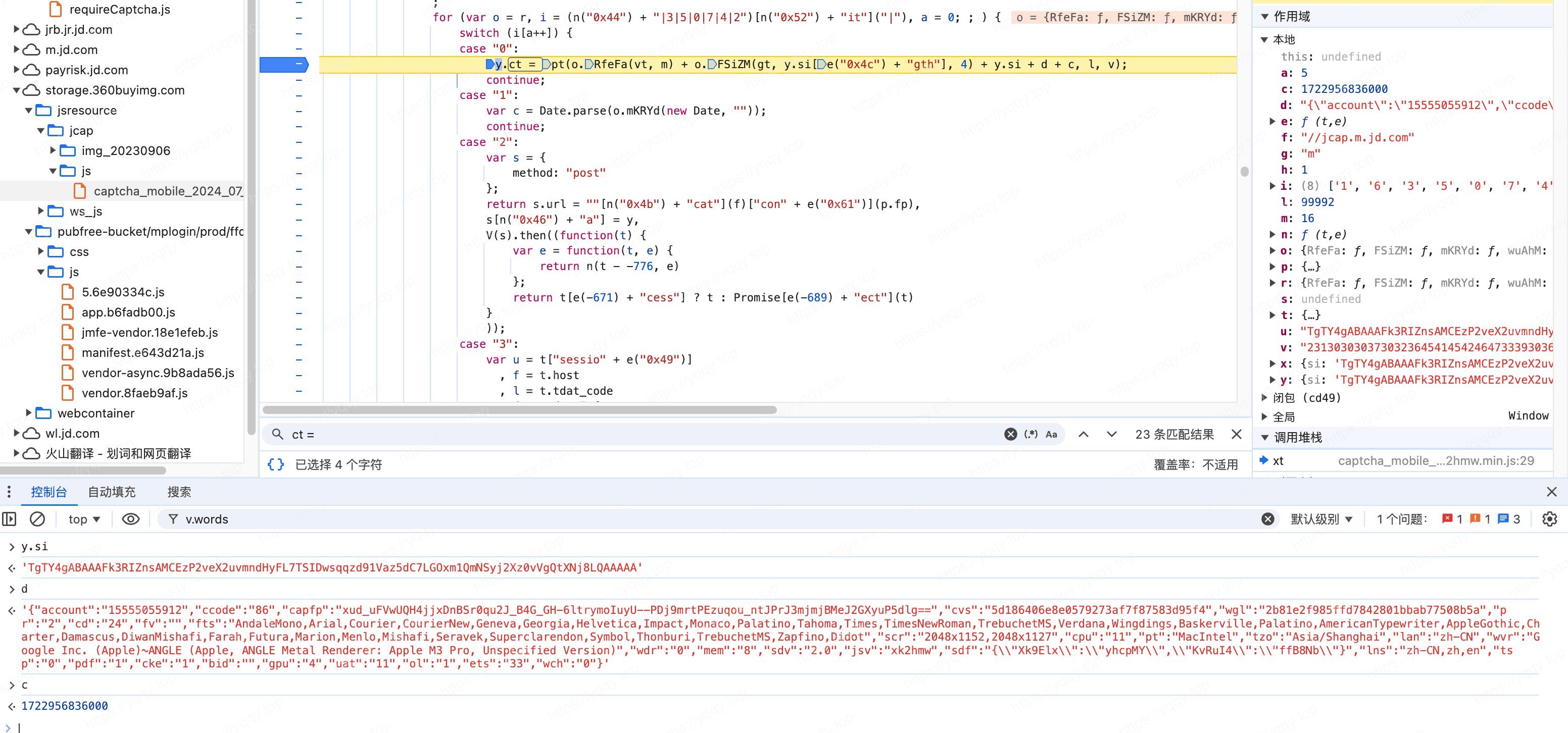
接着看o.FSiZM(gt, y.si[e("0x4c") + "gth"], 4)

其中FSiZM函数接收3个参数，其内部实现是t(e, n)，也就是可以变成o.FSiZM(gt(y.si[e("0x4c") + "gth"], 4))
e("0x4c") + "gth"，执行得出length，所以又可以变成o.FSiZM(gt(y.si["length"], 4))
那么gt函数是啥？扣一下

function gt(t, e) {
    for (let o = t.toString().length; o < e;) {
        t = "0" + t;
        o++;
    }
    return t
}

再往前是o.RfeFa(vt, m)，搜一下m是什么，m=时间戳%19

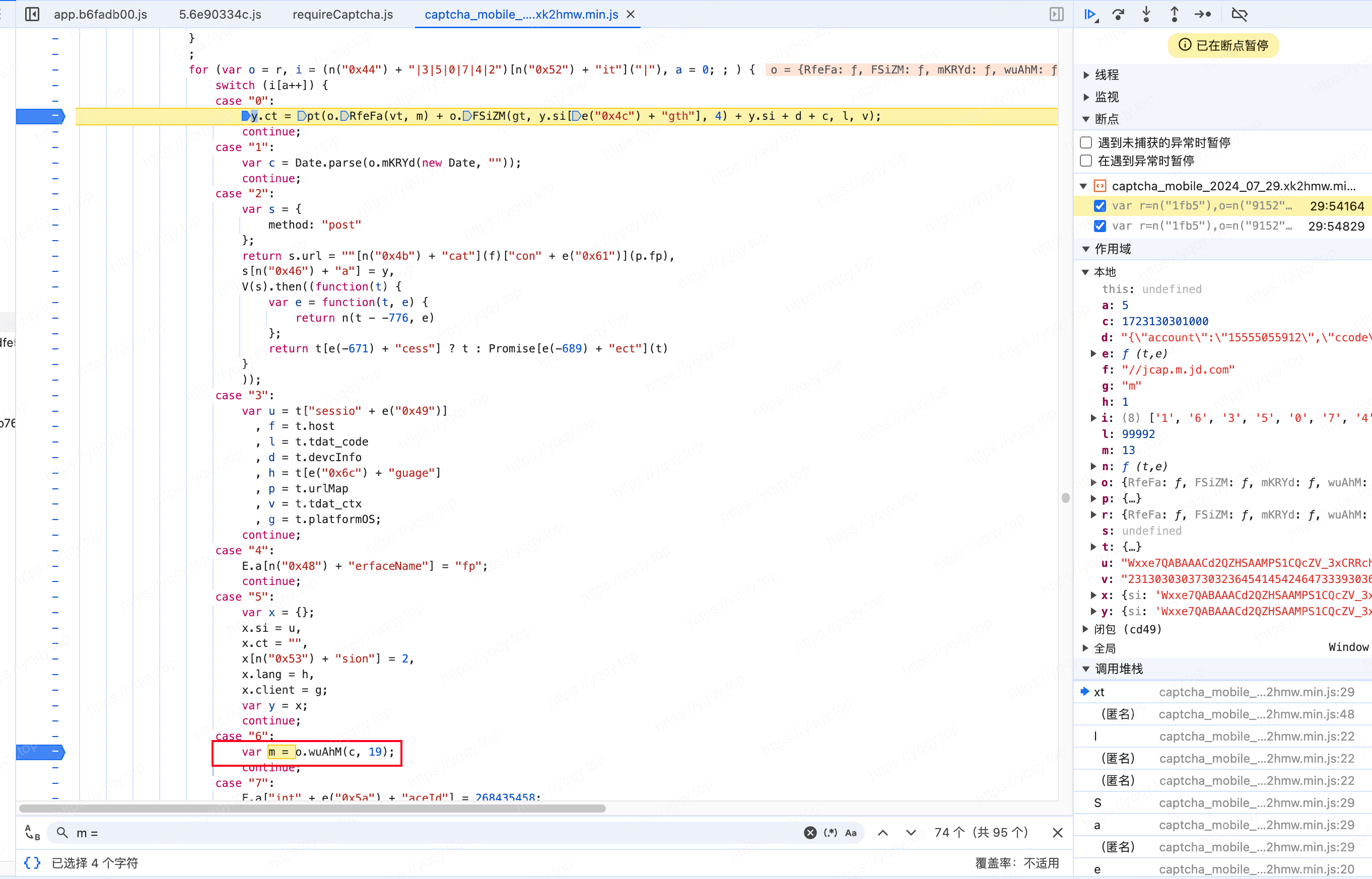
vt函数也同理，扣一下算法

function vt(t) {
    for (var e = function (t, e) {
        return a(t - -322, e)
    }, n = {
        kuqKR: function (t, e) {
            return t < e
        }
    }, r = ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "w", "x", "y", "z"], o = "", i = 0; n.kuqKR(i, t); i++) {
        o += r[Math.floor(35 * Math.random())]
    }
    return o
}

o.RfeFa和FSiZM一样，等于vt(m)

最后只差pt方法了，跟个断点走进去。return 后面跟着一个三元表达式，两个结果分别查看一下

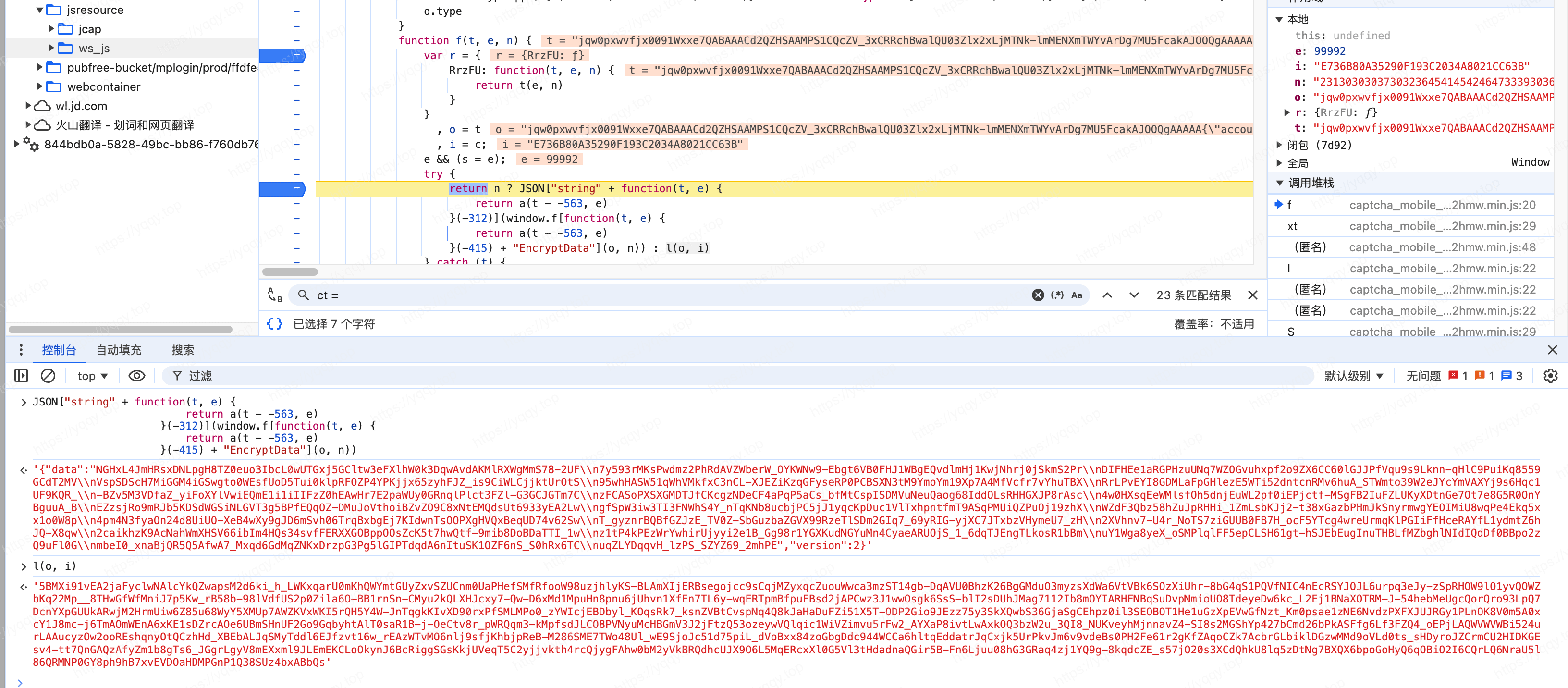
根据结果断定是前一种，拆开第一种发现，前面是一个JSON.stringify()，后面是一个加密函数

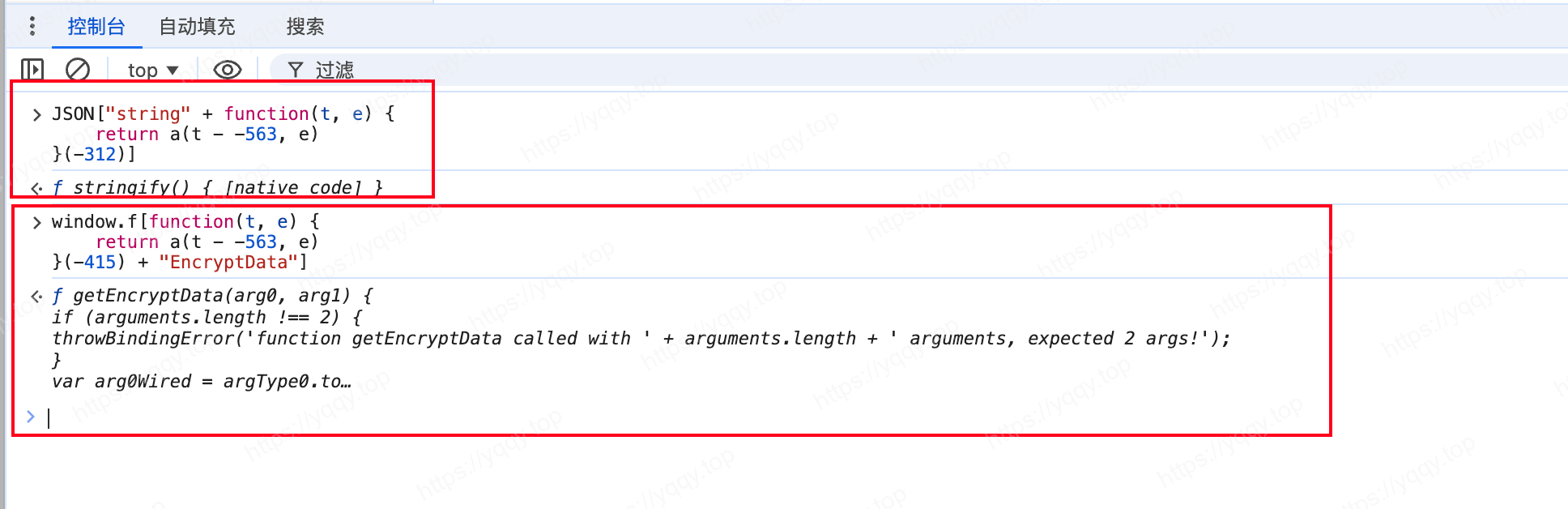
继续跟进去加密函数，未完待续...

某东M端登录滑块分析学习 ​

分析目标 ​

抓包分析 ​

逆向分析 ​

1.jcapsid - risk_jd[fp] ​

2.jcapsid - risk_jd[jstub] ​

3.fp - ct ​

4.check - tk、ct ​